Learn to Play

Shoot the target with your mighty cannon - or whatever your weapon happens to be. Write your mathematical function in the input box in the top left corner using either the on-screen buttons or your keyboard.

Straight lines

Straight lines are fairly easy. They are generally on the form y = ax+b. a is the slope of the line, and b says where the line intersects on the Y-axis. Since functions in WoMI always intersects the Y-axis in 0, you can ignore this. Only the a matters.

The slope a is the ratio between x and y. For each unit the line changes along the X-axis, it also changes along the Y-axis. This is written mathematically as a = 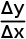. "Δ", the greek letter "delta", means "difference in" in mathemathics. So this reads "difference in Y divided by difference in X".

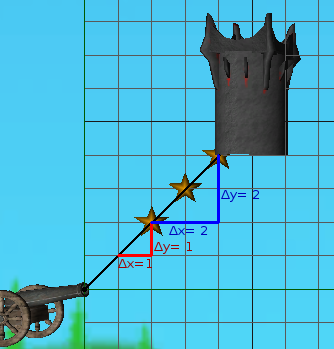
In the above image, two different Δx-es are used. They both give the same slope a when inserted into the formula. 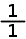and 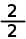both gives a = 1. Let's look at another slope:

Here we use Δx = 2, and see that Δy = -1. This means a = 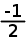, or -0.5 if you prefer decimals. WoMI handles both -1/2*x and -0.5x.

If you for some reason want the slope to be a specific angle, you can use the tan function. In this case, a = tan(angle). Be sure to use the right angle unit (degrees or radians), setable in the options menu. If you for some reason want the angle of a slope, use the atan function. angle = atan(a)

Sine waves

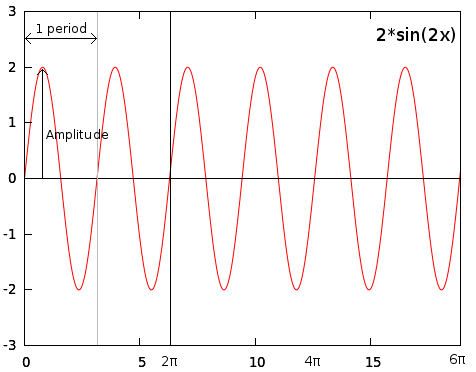
A sine wave is a periodic wave that is closely related to both triangles and circles. They are generally on the format a*sin(p-fx), where a is the amplitude, which is how tall the wave is, p is the phase shift modifier, which defines where on the wave a period should start, and f is the frequency modifier, defining how long each period is.

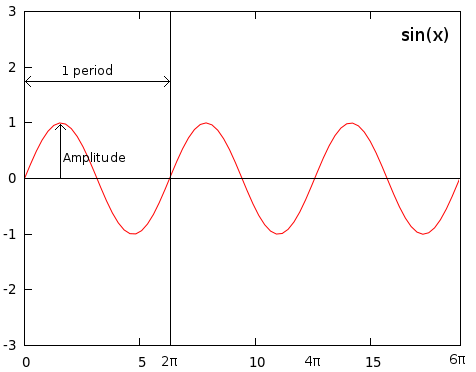
In WoMI, we focus only on a and f. If we make a=2, the wave would go twice as high, and twice as low.

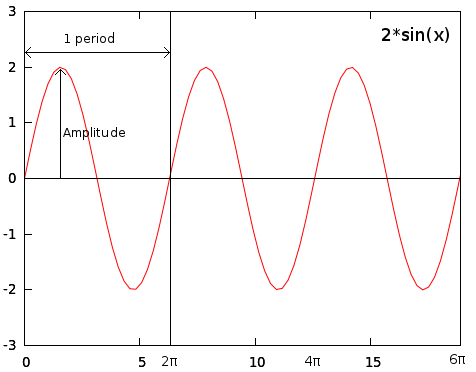
The frequency modifier f defines how many periods will fit between x = 0 and x = 2π if you use radians, or x = 0 and x = 360 if you use degrees.

a, f and p can also be functions, in which case we get so-called "Amplitude modulation" (AM), "Frequency Modulation" (FM), and "Phase Modulation" (PM), which you may recognize from radios. Below is an example of amplitude modulation:

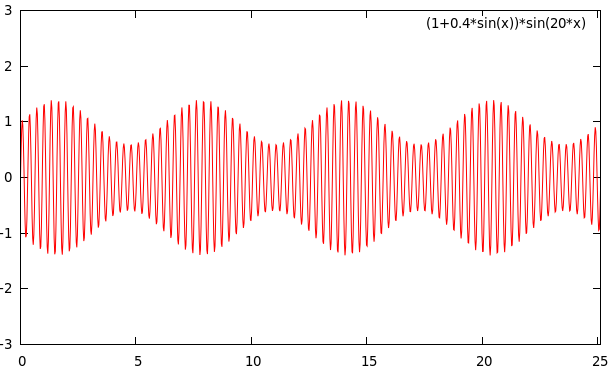
Here, we have a sine wave with a frequency of 20, with the function 1+0.4sin(x) as amplitude.